Introduction
- We are currently recruiting research members for our doctoral program. We are especially looking for individuals who are interested in vibration analysis, visualization, and design in fields such as automobiles, structures, and fluid dynamics, and who are eager to take the initiative in research and write first-author papers. If you are interested, please contact us at 【vib.eng.lab.kochi△gmail.com (Please change △to @)】.
- In this laboratory, doctoral students have the opportunity to engage in research in the field of vibration engineering. In particular, we offer a wide range of research themes related to vibration imaging, vibration-based design, and fault diagnosis. Examples of these themes are presented on this page.
- Basic knowledge of vibration engineering and MATLAB programming skills are required.
- Available Equipment and Facilities for Use: Electrodynamic shaker, Complete set of vibration measurement instruments, Workstations for computer simulation, Fluid analysis software, Structural analysis software, Full set of vibration mode analysis equipment, High-speed cameras, High-frequency visualization system including strobe lighting, Ultrasonic testing equipment, and High-frequency data loggers.
- For details on the scholarship program, please refer to the URL
>Research Topics
- Rotating machinery such as automotive engines and jet engines are constantly exposed to vibrations, which significantly affect their performance, product lifespan, and safety. Therefore, vibration measurement is essential in practical settings such as design, manufacturing, and maintenance.
- In these environments, it is common to use contact-type sensors known as accelerometers for measurement. However, these sensors must be manually attached, which introduces challenges in terms of the time and effort required for installation and wiring. Furthermore, because it is difficult to capture the spatial distribution of the vibration modes, vibration-based design can be challenging in some cases.
- On the other hand, by using an image-based measurement technique known as Digital Image Correlation (DIC), which tracks marker points, it is possible to measure the vibration of a target object in a non-contact, full-field manner without attaching sensors. However, measuring high-speed vibrations requires the use of high-speed cameras. As the frame rate increases, the spatial resolution (i.e., the number of pixels) typically decreases, making it difficult to capture both wide-area and fine-scale vibrations simultaneously.
- To address this issue, our research group has developed a novel method called Compressed Sensing DIC, which combines DIC with two data science techniques: Compressed Sensing and Proper Orthogonal Decomposition (POD), a type of modal decomposition method.
- Using this method, we successfully measured high-frequency vibrations in the range of 150–1130 Hz during steady-state vibration tests, based on images captured at only 10 Hz, as shown in Figure 1 [1-1].
- Furthermore, by improving the basis functions used for observation and introducing order-based bases derived from rotational information, we have successfully measured the actual operational vibrations of an engine. Figure 2 shows the results of measuring an engine intake pipe and an automobile bonnet using the developed method. As shown in the center of the figure, the deformation shapes of the intake pipe and bonnet were captured in detail and over a wide area
- Additionally, as shown on the right side of the figure, the vibration spectrum measured by our method closely matches that obtained from an accelerometer. The proposed method using the order-based basis achieved a measurement error of only 1.9%, a significant improvement over the conventional Fourier basis approach, which had an error of 97.9%.
- In the case of the bonnet vibration, the measurement error was relatively high at 26.2%; however, this is presumed to be due to the fact that the vibration was extremely small—on the order of sub-micrometers, comparable to the wavelength of visible light—leading to decreased measurement accuracy due to factors such as light refraction [1-2].
- Through this research, full-field measurement of operational vibrations—previously unmeasurable—has become possible over a wide area (1 m²), at high frequencies (several hundred Hz), and with small amplitudes (several micrometers).
- Moving forward, we aim to further advance the vibration design of engines, vehicle bodies, and structures using this method. Additionally, by extending the developed approach, we plan to measure the natural frequencies and mode shapes of structures and integrate these results with numerical simulation models.
- Factories operate with a wide variety of machinery, all of which are inevitably subject to failure due to material defects, fatigue, and aging. Machinery failure can lead to equipment shutdowns and significant economic losses, making fault diagnosis and maintenance to preserve normal operating conditions critically important.
- Diagnostic methods based on sound and vibration are robust and capable of early fault detection. As a result, they have been widely applied to components such as gears, propellers, and bearings. However, there are notable challenges:
- To overcome these issues, our laboratory is engaged in the following lines of research.
- We are conducting research aimed at significantly reducing the data required for vibration measurement by applying compressed sensing. An overview of this approach is shown in Figure 2-1. As illustrated on the right side of the figure, we have successfully compressed both the data volume and measurement frequency to approximately 1/100 compared to full sampling.
- Since the method achieves measurement accuracy comparable to full sampling, it enables the evaluation of fault diagnosis indicators based on spectral information in the 50–500 Hz range, as shown on the left side of the figure. This allows for effective fault diagnosis of components such as propellers using low-volume data.
- Furthermore, because the required measurement frequency is reduced, high-speed data loggers are no longer necessary, making low-cost measurement possible.
- Currently, we are working with an industry partner to commercialize this logger technology.
- In press machines, loud processing noise is generated during cutting, and analyzing this noise has the potential to enable fault detection. However, when analyzing such processing sounds, cutting out the time segments before and after the operation to perform FFT—intended to eliminate environmental noise—leads to degraded spectral resolution. As a result, vibration components and eigenfrequencies cannot be effectively extracted.
- To address this issue, we applied **Dynamic Mode Decomposition (DMD)**—a technique primarily used in fluid dynamics—to acoustic signal analysis, thereby improving spectral resolution. Furthermore, as shown at the top of Figure 2-2, we enhanced the method by incorporating **L1 norm minimization**, enabling automatic extraction of dominant components.
- Thanks to this improvement, we were able to clearly identify components around 100 Hz, which could not be resolved using FFT alone. Comparing these results with eigenvalue analysis via FEM revealed that the 80–120 Hz components originated from vertical vibrations of the plate, while the components around 200 Hz were due to horizontal vibrations. This suggests that an abnormal horizontal excitation force was generated due to a defect in the die, resulting in the 200 Hz anomalous sound.
- Through this approach, we achieved high-precision fault diagnosis of press machines. Going forward, we plan to apply this method to the diagnosis of other types of machinery.
- We are applying the compressed sensing and POD fusion technology developed in Research Theme ① to flow field measurement using Particle Image Velocimetry (PIV). As shown in Figure __, this method enables the visualization and measurement of oscillatory flows, such as Kármán vortices, at a resolution several times higher than that of conventional high-speed cameras.
- This technique is expected to significantly enhance flow field measurements around aircraft and vehicle bodies.
- In the future, we plan to apply this approach to the measurement of acoustic flows and pulsating flows within piping systems.
- Under construction
- Under construction
Research Topic 1: Full-Field Vibration Measurement of High-Speed Vibrations Using Compressed sensing DIC
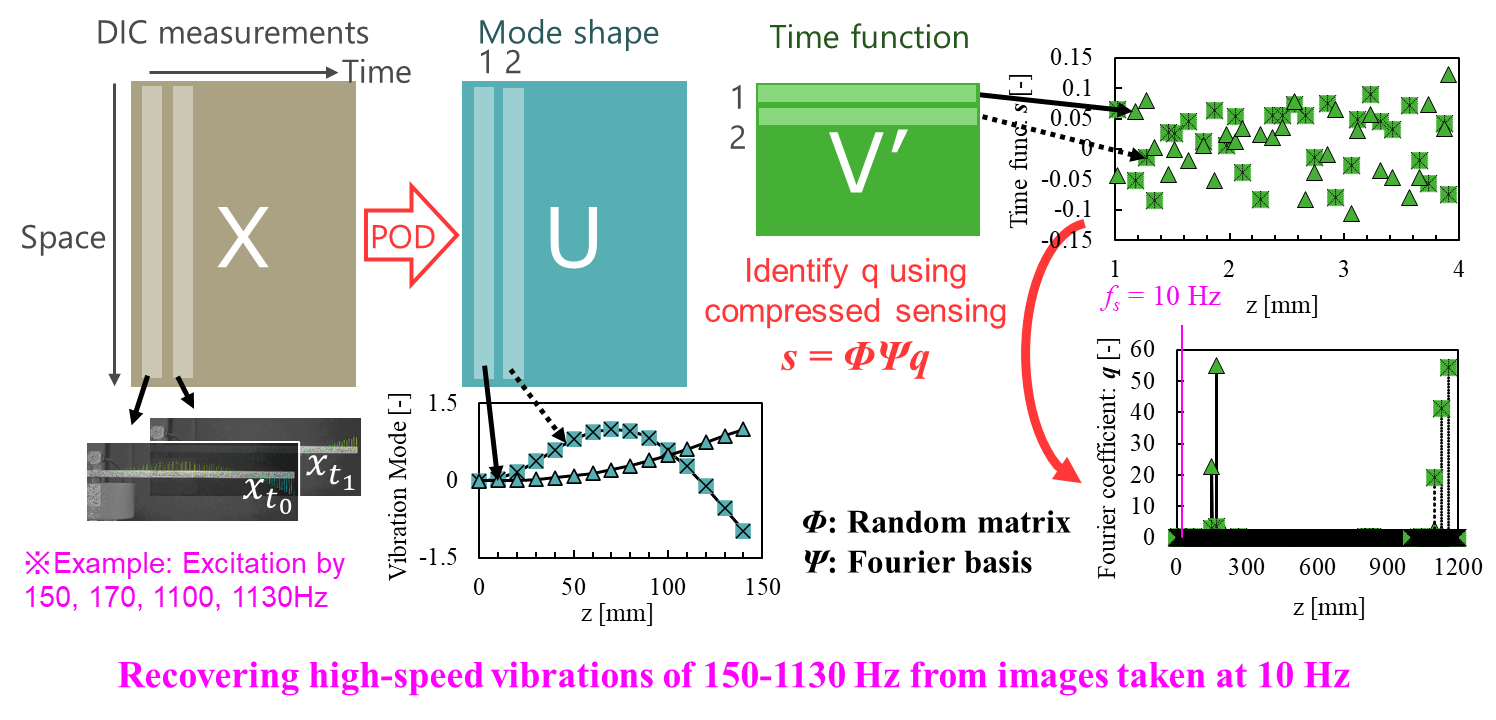
Figure 1-1: Results of reconstructing the vibration information of a beam by applying POD and compressed sensing to measurement data obtained via DIC. Vibrations more than 100 times faster than the imaging frame rate were successfully reconstructed.
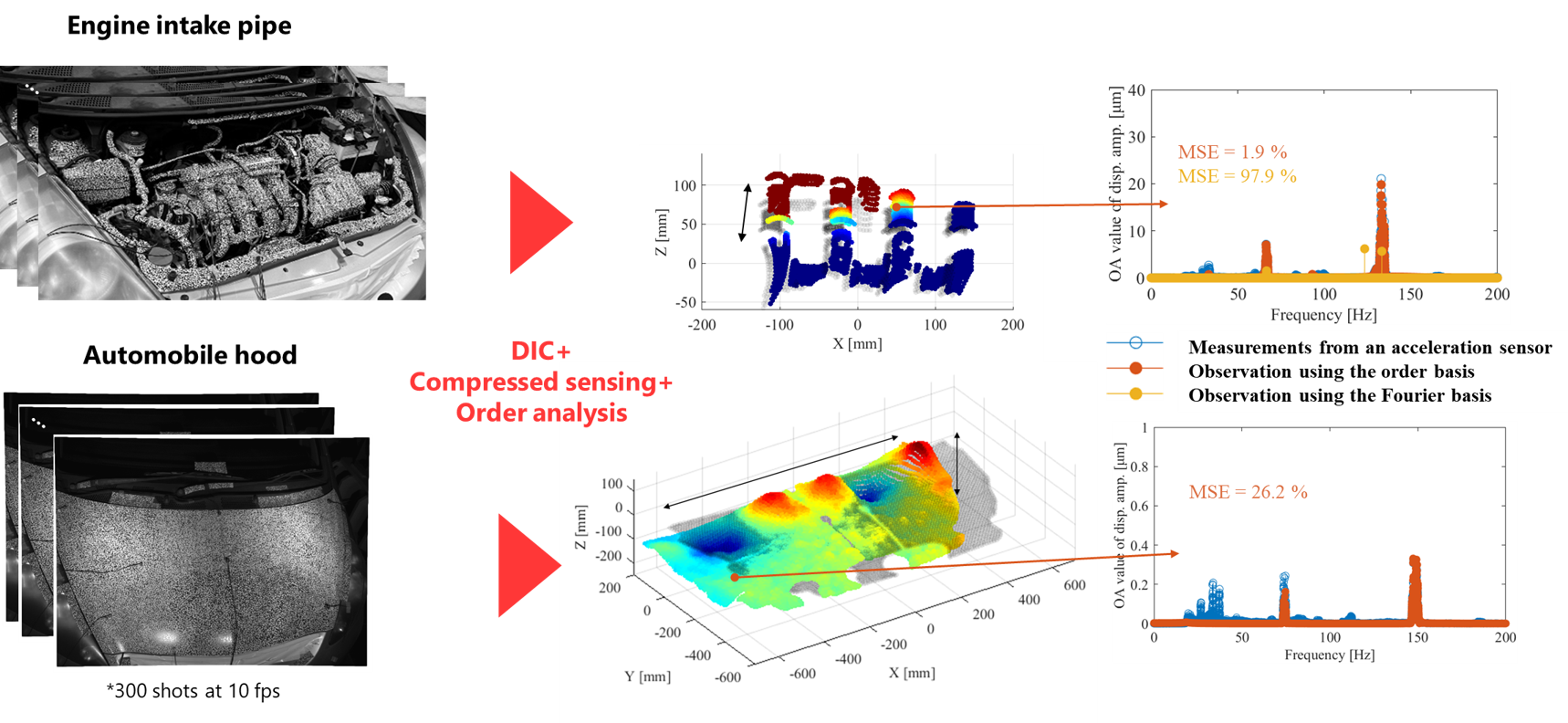
Figure 1-2 The results of measuring the vibration of the engine intake pipe and bonnet using the proposed method
[1-1] Kato, Y., & Watahiki, S. (2023). Vibration mode identification method for structures using image correlation and compressed sensing. Mechanical Systems and Signal Processing, 199, 110495.
[1-2] Kato, Y., & Watahiki, S. (2025). Full-field measurements of high-frequency micro-vibration under operational conditions using sub-Nyquist-rate 3D-DIC and compressed sensing with order analysis. Mechanical Systems and Signal Processing, 224, 112179.
Research topic 2: Fault Diagnosis of Machinery Using Vibration
[Issue 1] The data volume tends to become large, making system operation and data management difficult.
[Issue 2] In the case of impact vibrations, such as those from presses, the vibration spectrum becomes smeared, which makes diagnosis challenging.
[Issue 1]
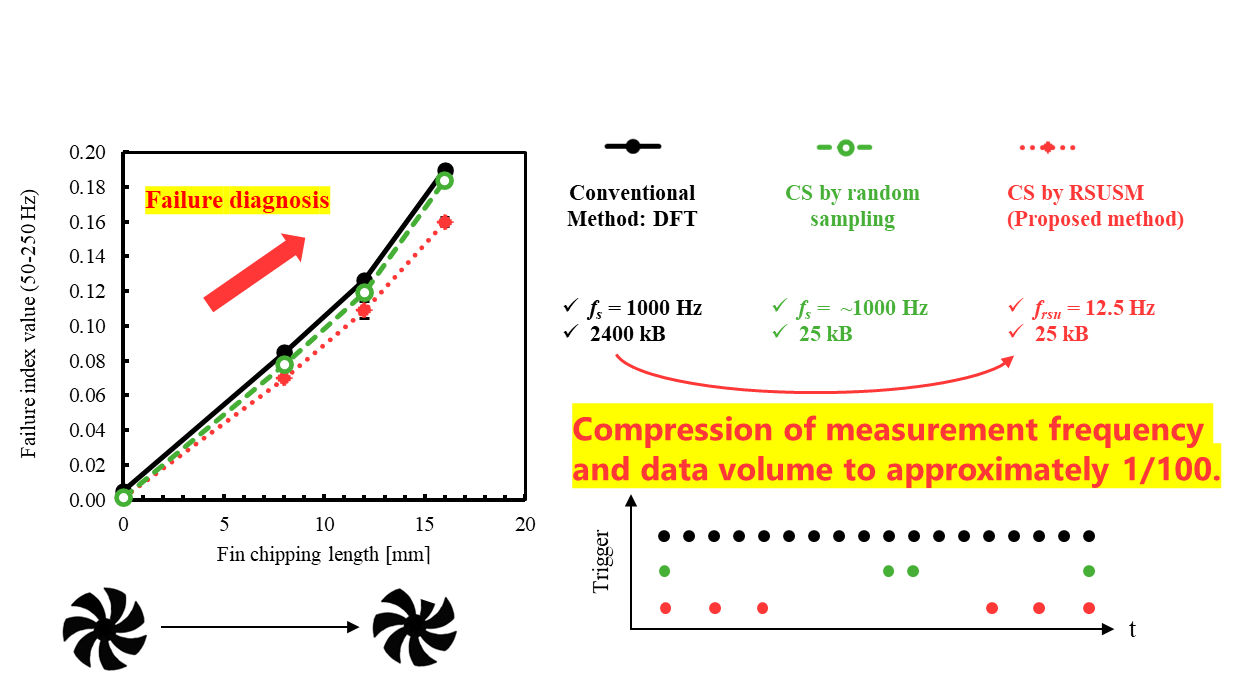
Figure 2-1 Fault Diagnosis of Propellers Using Compressed Sensing
[2-1] Kato, Y. (2022). Fault diagnosis of a propeller using sub-nyquist sampling and compressed sensing. IEEE Access, 10, 16969-16976.
[Issure 2]
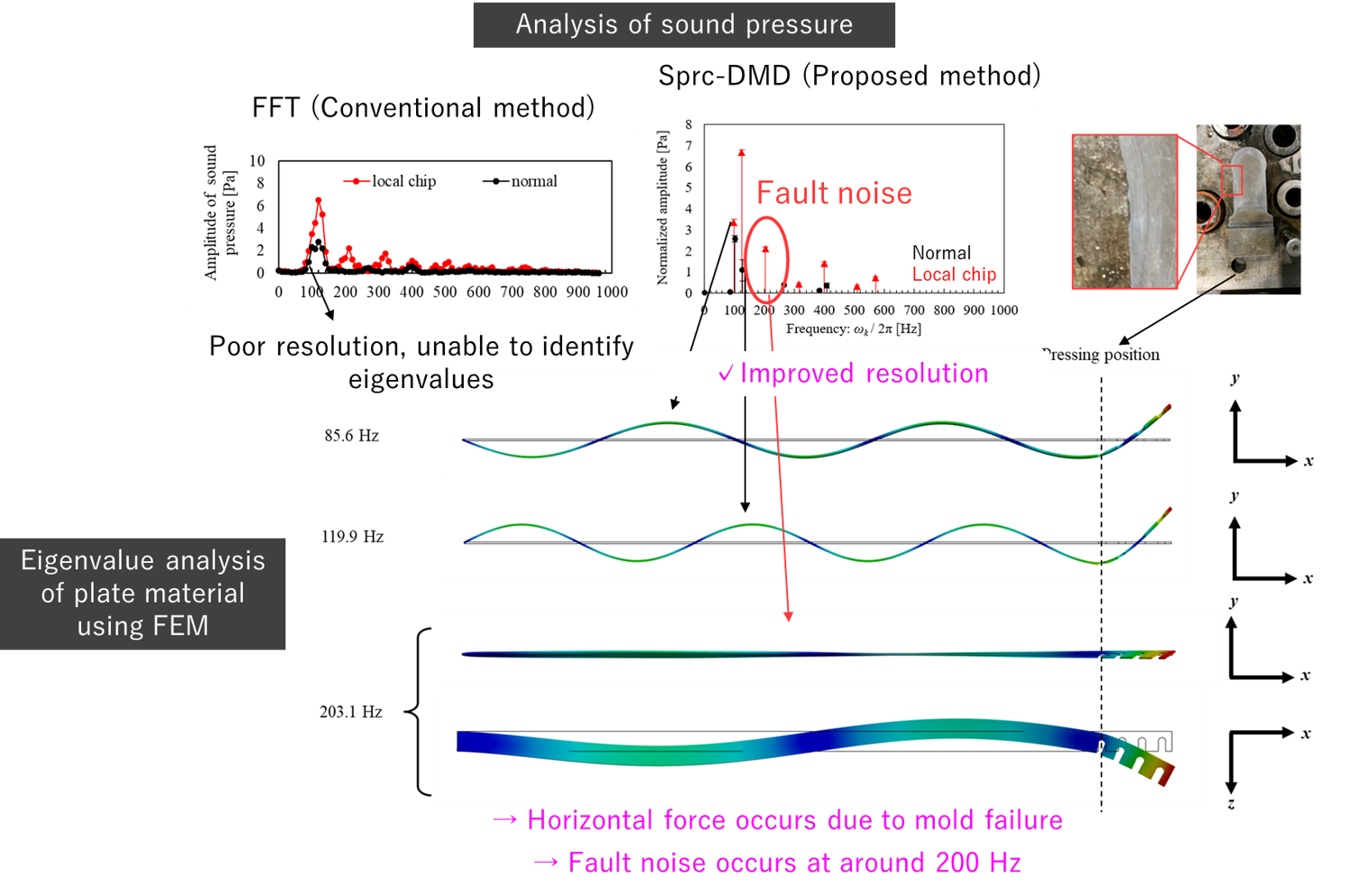
Figure 2-2 Fault diagnosis of press dies using DMD
[2-2] Kato, Y., & Kumagai, R. (2023). Fault diagnosis of press dies using dynamic mode decomposition of a sound signal. Journal of Advanced Mechanical Design, Systems, and Manufacturing, 17(3), JAMDSM0040-JAMDSM0040.
Research topic 3: Flow Field Measurement Using Compressed sensing PIV
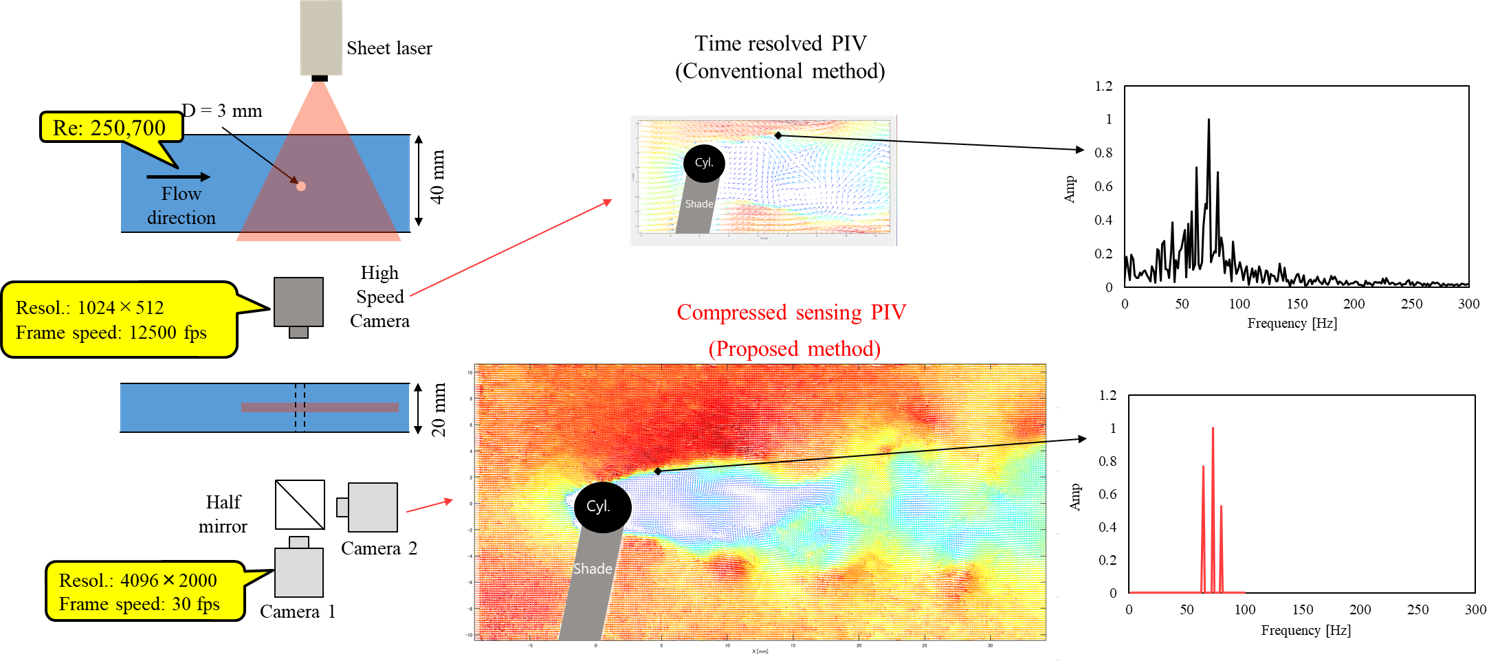
Figure 3-1 Visualization measurements of Karman vortex using compressed sensing PIV
[3-1] Kato, Y. (2025). High-resolution visualization measurement of vortex-shedding at high frequencies using sub-Nyquist-rate PIV and compressed sensing. Journal of Flow Visualization and Image Processing, 32(1).
Research topic 4: Flow and heat transfer characteristics of pulsating flow
[4-1] Kato, Y., Guo, G., Kamigaki, M., Fujimoto, K., Kawaguchi, M., Nishida, K., ... & Ogata, Y. (2022). Correlation Between Wall Heat Transfer and Characteristics of Pulsating Flow in A Rectangular Tube toward an Automobile Exhaust System. In Proceedings of the 8th World Congress on Mechanical, Chemical, and Material Engineering, Prague, Czech Republic (Vol. 31).
[4-2] Kato, Y., Guo, G., Kamigaki, M., Fujimoto, K., Kawaguchi, M., Nishida, K., ... & Ogata, Y. (2023). An Examination of Heat Transfer Dynamics in Pulsating Air Flow within Pipes: Implications for Automotive Exhaust Engines. International Journal of Heat & Technology, 41(4).
[4-3] Kato, Y., Fujimoto, K., Guo, G., Kawaguchi, M., Kamigaki, M., Koutoku, M., ... & Ogata, Y. (2023). Heat transfer characteristics of turbulent flow in double-90-bend pipes. Energies, 16(21), 7314.
[4-4] Kato, Y., Fujimoto, K., Yanagida, H., Nakamura, K., & Ogata, Y. (2025). Effect of the flow structure of pulsating turbulent flow in a duct with a double 90° bend on convective heat transfer at the wall. International Communications in Heat and Mass Transfer, 164, 108795.
Research topic 5: Development of soundproofing device using acoustic black holes
※In addition to the above, we are currently working on one vibration design theme, two image vibration measurement themes, and one anomaly detection theme. We are also conducting joint research with companies and universities.
Methods
Compressed sensing
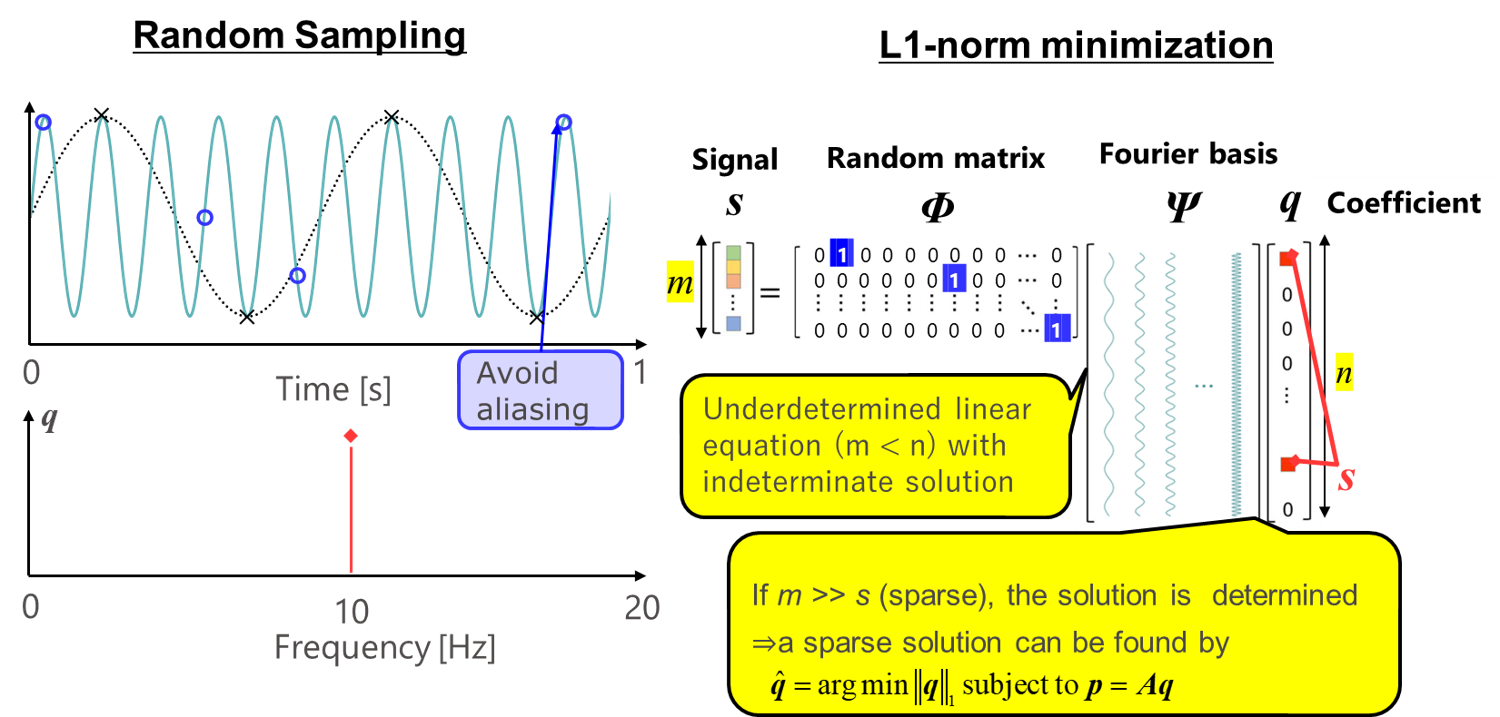
Figure A: Overview of compressed sensing
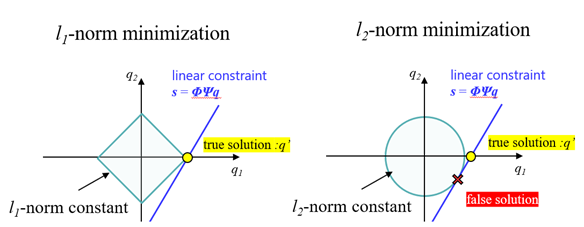
Figure B: Solving underdetermined problems using L1 norm minimization
[A] *D. L. Donoho and J. Tanner, in IEEE Transactions on Information Theory, vol. 56, no. 4, pp. 2002-2016, April 2010
DIC(Digital Image Correlation)
PIV(Particle Image Velocimetry)
POD(Proper Orthogonal Decomposition)
DMD(Dynamic Mode Decomposition)
Applications
Research findings have been implemented in the following areas:
- Vibration design of automobile bodies and tires
- Fault diagnosis in factories and infrastructure
- Optimization of fluid heat transfer in automobile exhaust pipes and piping systems