はじめに
- 大学(学士)や大学院(修士/博士課程)での研究メンバーを募集しています。構造物や流体の振動解析/可視化の基礎研究に興味がある方、または自動車や航空機の振動設計問題に関する応用研究に興味がある方を特に募集しています。興味がある方は、【vib.eng.lab.kochi△gmail.com(△を@に変えてください)】までご連絡ください。
- また、共同研究にご興味がある方もお気軽にお問い合わせください。
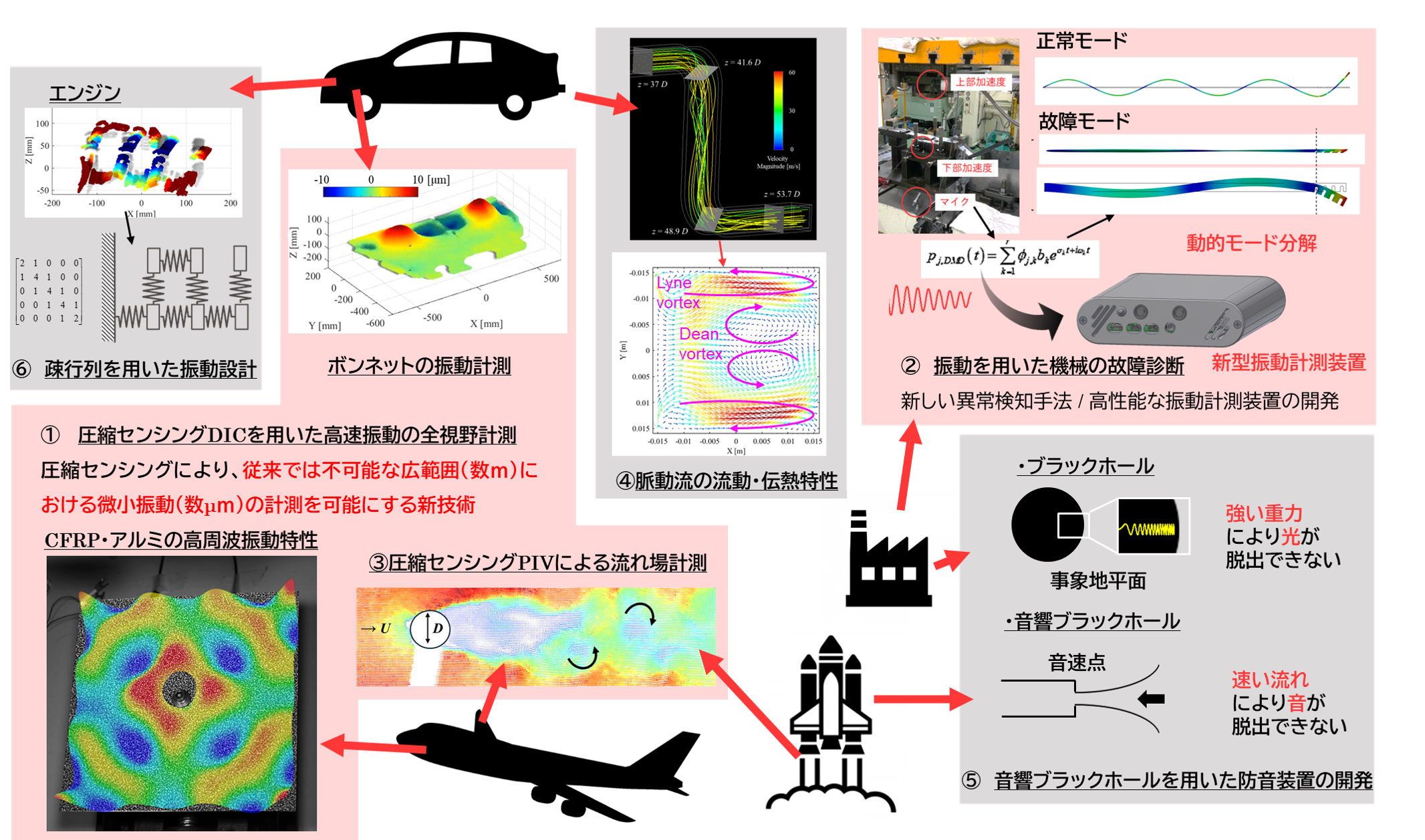
研究トピック
- 自動車用エンジンやジェットエンジン等の回転機械は絶えず振動にさらされており、振動がそれらの性能や製品寿命、安全性を大きく左右します。そのため、設計・製造・保守といった現場においては振動の計測が不可欠です。これらの現場では、加速度センサと呼ばれる接触式のセンサによる計測を行うことが一般的です。しかし、センサは手作業で貼り付ける必要があり、設置や配線等にかかる手間と労力が課題となっていました。また、空間的な振動形状の把握が難しいことから、振動設計が困難となるケースがありました。
- 一方、マーカーの点をトラッキングするデジタル画像相関法(DIC)と呼ばれる画像計測技術を用いることで、センサを貼り付けることなく対象物の振動を非接触かつ面的に計測することが可能になります。しかし、高速振動の計測にはハイスピードカメラが必須であり、撮影速度を上げるほど画素数が低下するため、広範囲かつ微小な振動を計測できないという課題がありました。この課題を解決するため、当研究グループはDICに「圧縮センシング*1」と「POD」(モード分解手法の一種)という二つのデータサイエンス技術を組み合わせた新手法であるCompressed Sensing DICを開発しました)。この手法により、図1に示すとおり10 Hzで撮影した画像をもとに定常振動試験において出現した150-1130 Hzの高速振動を計測することに成功しています[1-1]。
- また、観測に用いる基底を改良し、回転情報を基にした次数基底を用いることで、エンジンの実稼働振動の計測にも成功しています。図2は、開発した手法によりエンジン吸気配管や自動車ボンネットを計測した結果です。同図中央部に示すとおり、吸気配管やボンネットの変形形状が詳細かつ広範囲に計測できていることが分かります。また、同図右側に示すとおり、加速度センサと同様な振動スペクトルを計測できていることが分かります。提案した次数基底を用いた手法の計測誤差は1.9 %であり、従来法のフーリエ基底による観測による誤差97.9%と比べて大幅に精度を改善することができました。ボンネットの振動については26.2%と計測誤差が大きくなりましたが、これはサブマイクロメーター(可視光の波長と同じオーダー)の微小振動であったため、光の屈折などにより画像計測精度が悪化したことに起因すると推定されています[1-2]。
- 本研究により、これまで計測できなかった広範囲(1m2)・高周波(数百Hz)・微小振幅(数μm)の実稼働振動の全視野計測が可能となりました。今後は、本手法によりエンジンや車体、構造物の振動設計の更なる高度化を目指していきます。また、開発した手法を拡張することで、構造物の固有振動数や固有モードの計測、数値計算モデルとの融合を行う予定です。
- 工場は様々な機械により稼働していますが、機械は材料の欠陥や疲労,経年劣化などにより必ず故障します。機械の故障は設備の停止を招き、経済的損失をもたらすため,故障診断を実施し機械を正常な状態に保全することが非常に重要です。音や振動に基づく診断方法はロバストで故障を早期に発見できるため、ギアやプロペラ、軸受などを対象に幅広く活用されてきました。しかし、データ容量が大きくなり運用が難しくなる[課題1]、プレス機などの衝撃振動の診断においてはスペクトルが鈍ることで診断が困難になる、という問題がありました。当研究室ではこの課題を克服すべく、下記の様な研究に取り組んでいます。
- 圧縮センシングを用いて、振動計測に必要なデータ量を大幅に低減する研究に取り組んでいます。図2-1にその概要を示します。図右側に示す通り、フルサンプリングと比べて、データ容量や計測周波数を1/100に圧縮することに成功しています。フルサンプリングと同様の計測ができるため、図左側に示すように50-500 Hzのスペクトル情報を基に計算する故障診断の指標値を評価でき、低データ容量のプロペラの故障診断が実現できます。また、計測周波数も低減できているため、高速ロガーが不要になり、安価な計測が実現できます。
- 現在は共同研究先の企業とロガーの製品化に取り組んでいます。
- プレス機においては切断の際に大きな加工音が発生するため、これを分析することで故障検知できる可能性があります。しかし、加工音を分析する際、周囲環境の影響を排除するために加工前後を切り出してFFTを実施すると、スペクトルの分解能が悪化し、振動成分/固有値が上手く抽出できない問題がありました。そこで、流体解析で主に使用されている動的モード分解(DMD)を音の分析に適用することで、スペクトル分解能を改善しました。更に、図2-2上部に示すように、L1ノルム最小化により支配的な成分を自動抽出できるよう改良しました。これにより、図に示す通りFFTでは分解できなかった100 Hz前後の成分を、明瞭に区別して抽出できるようになりました。この結果とFEMによる固有値解析結果を比較すると、80-120 Hzの成分は板の垂直方向振動に由来し、200 Hz前後の成分は板の水平方向振動に由来することが分かりました。金型の以上により水平方向加振力が発生し、200 Hzの異常音が発生したと推定できます。
- 以上により、プレス機の精密な故障診断を実現することができました。今後はこの手法を他の機器の故障診断に応用する予定です。
- 研究テーマ①で開発した圧縮センシングとPODの融合技術を、PIVによる流れ場計測に応用しています。図 に示すように、通常のハイスピードカメラの 倍の解像度でカルマン渦のような振動流れを可視化計測できるようになりました。この手法により、航空機や車体周囲の流れ場計測の高度化が期待されます。
- 圧縮センシングを用いて、振動計測に必要なデータ量を大幅に低減する研究に取り組んでいます。図2-1にその概要を示します。図右側に示す通り、フルサンプリングと比べて、データ容量や計測周波数を1/100に圧縮することに成功しています。フルサンプリングと同様の計測ができるため、図左側に示すように50-500 Hzのスペクトル情報を基に計算する故障診断の指標値を評価でき、低データ容量のプロペラの故障診断が実現できます。また、計測周波数も低減できているため、高速ロガーが不要になり、安価な計測が実現できます。
- 今後は、音響流や配管内脈動流の計測に応用する予定です。
- 作成中
- 作成中
研究テーマ①:圧縮センシングDICを用いた高速振動の全視野振動計測
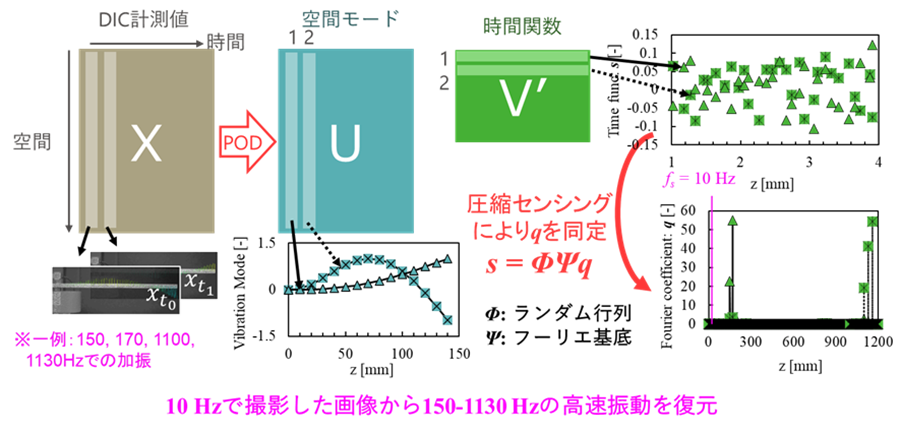
図1-1 DICによる計測データにPODと圧縮センシングを適用することで、梁の振動情報を復元した結果。撮影速度より100倍以上高速な振動を復元できている。
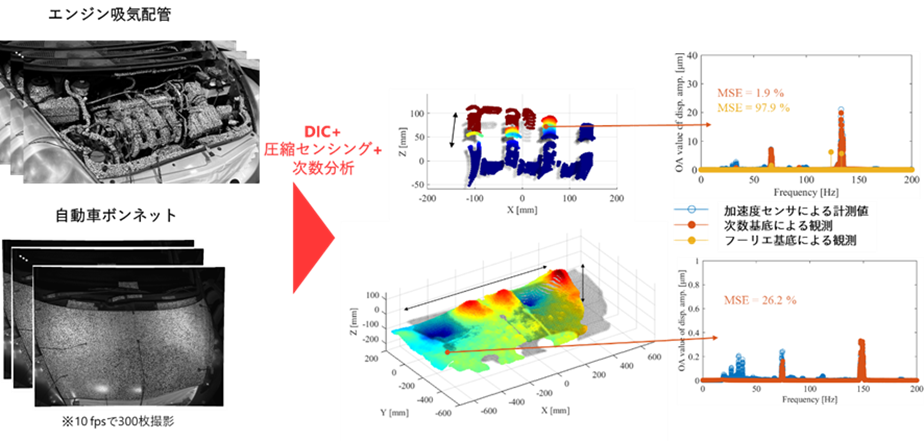
図1-2 開発した手法によりエンジン吸気配管とボンネットの振動を計測した結果
[1-1] Kato, Y., & Watahiki, S. (2023). Vibration mode identification method for structures using image correlation and compressed sensing. Mechanical Systems and Signal Processing, 199, 110495.
[1-2] Kato, Y., & Watahiki, S. (2025). Full-field measurements of high-frequency micro-vibration under operational conditions using sub-Nyquist-rate 3D-DIC and compressed sensing with order analysis. Mechanical Systems and Signal Processing, 224, 112179.
研究テーマ②:振動を用いた機械の故障診断
[課題1に対する研究]
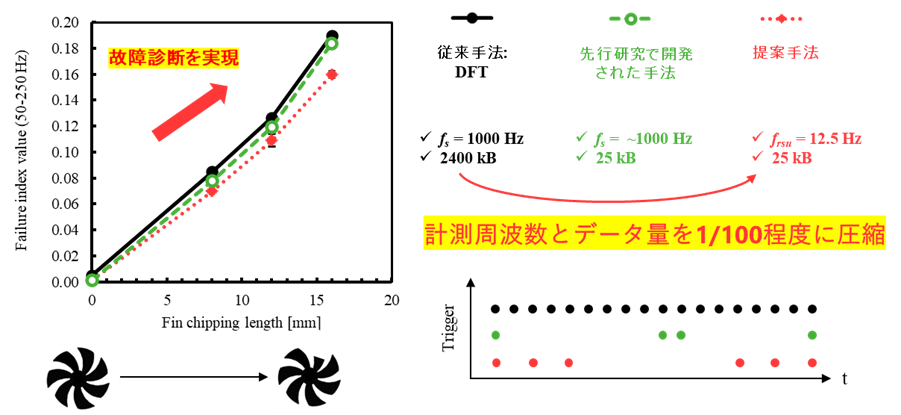
図2-1 圧縮センシングを用いたプロペラの故障診断
[2-1] Kato, Y. (2022). Fault diagnosis of a propeller using sub-nyquist sampling and compressed sensing. IEEE Access, 10, 16969-16976.
[課題2に対する研究]
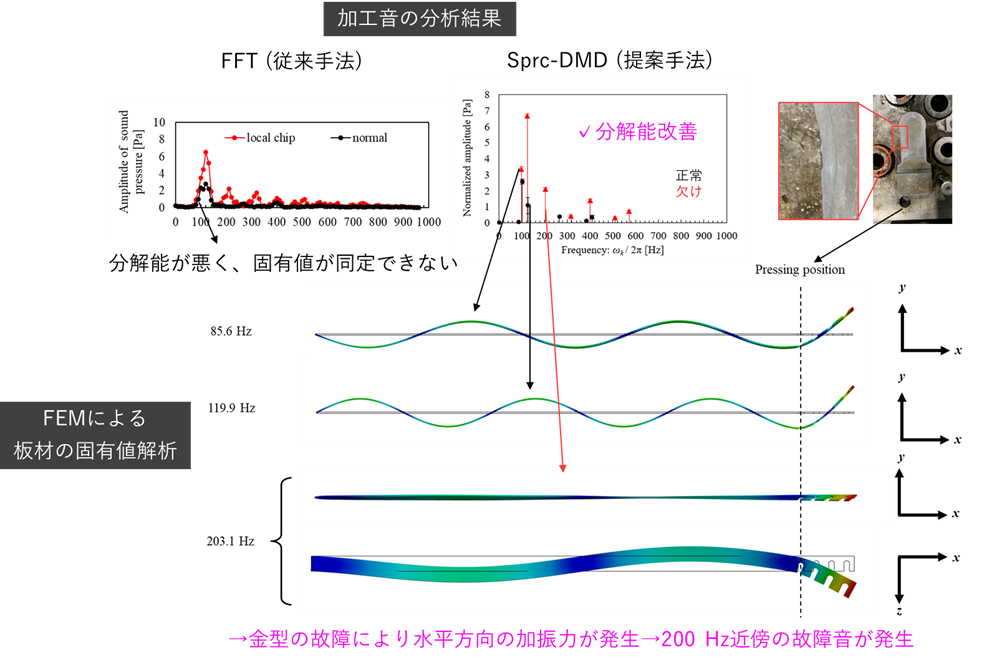
図2-2 DMDを用いたプレス金型の故障診断
[2-2] Kato, Y., & Kumagai, R. (2023). Fault diagnosis of press dies using dynamic mode decomposition of a sound signal. Journal of Advanced Mechanical Design, Systems, and Manufacturing, 17(3), JAMDSM0040-JAMDSM0040.
研究テーマ③:圧縮センシングPIVによる流れ場計測
[課題1に対する研究]

図3-1 圧縮センシングPIVを用いたカルマン渦の可視化計測
[3-1] Kato, Y. (2025). High-resolution visualization measurement of vortex-shedding at high frequencies using sub-Nyquist-rate PIV and compressed sensing. Journal of Flow Visualization and Image Processing, 32(1).
研究テーマ④:脈動流の流動・伝熱特性
[4-1] Kato, Y., Guo, G., Kamigaki, M., Fujimoto, K., Kawaguchi, M., Nishida, K., ... & Ogata, Y. (2022). Correlation Between Wall Heat Transfer and Characteristics of Pulsating Flow in A Rectangular Tube toward an Automobile Exhaust System. In Proceedings of the 8th World Congress on Mechanical, Chemical, and Material Engineering, Prague, Czech Republic (Vol. 31).
[4-2] Kato, Y., Guo, G., Kamigaki, M., Fujimoto, K., Kawaguchi, M., Nishida, K., ... & Ogata, Y. (2023). An Examination of Heat Transfer Dynamics in Pulsating Air Flow within Pipes: Implications for Automotive Exhaust Engines. International Journal of Heat & Technology, 41(4).
[4-3] Kato, Y., Fujimoto, K., Guo, G., Kawaguchi, M., Kamigaki, M., Koutoku, M., ... & Ogata, Y. (2023). Heat transfer characteristics of turbulent flow in double-90-bend pipes. Energies, 16(21), 7314.
[4-4] Kato, Y., Fujimoto, K., Yanagida, H., Nakamura, K., & Ogata, Y. (2025). Effect of the flow structure of pulsating turbulent flow in a duct with a double 90° bend on convective heat transfer at the wall. International Communications in Heat and Mass Transfer, 164, 108795.
研究テーマ⑤:音響ブラックホールを用いた防音装置の開発
※このほかにも振動設計のテーマが一つ、画像振動計測のテーマが二つ、異常検知のテーマが一つ進行中です。また、企業との共同研究や、大学間での共同研究も実施中です。
研究手法
圧縮センシング
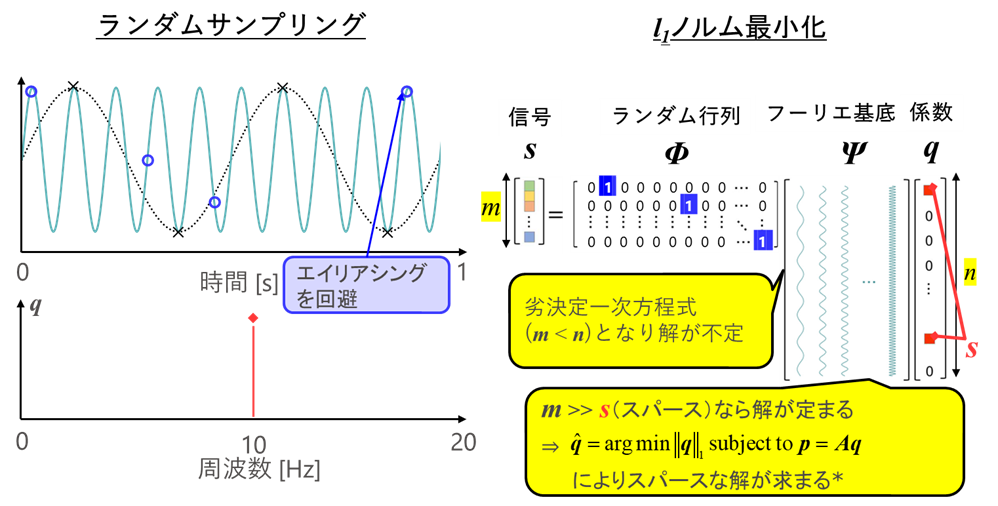
図A 圧縮センシングの概要
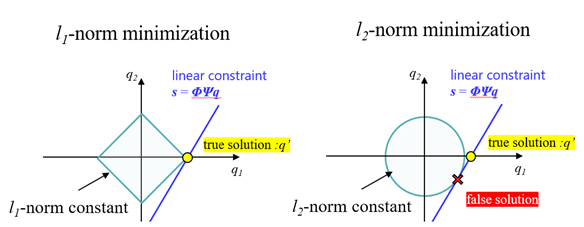
図B L1ノルム最小化を用いた劣決定問題の解法
[A] *D. L. Donoho and J. Tanner, in IEEE Transactions on Information Theory, vol. 56, no. 4, pp. 2002-2016, April 2010
DIC(Digital Image Correlation)
PIV(Particle Image Velocimetry)
POD(Proper Orthogonal Decomposition)
DMD(Dynamic Mode Decomposition)
応用事例
研究成果は以下のような実社会問題に応用されています:
- 自動車の車体やタイヤの振動設計
- 工場やインフラにおける故障診断
- 自動車排気管や配管系の流体伝熱最適化